Introduction

When comparing camera lenses, one of the most commonly discussed features is how “fast” a lens is—usually expressed in terms of f-numbers. But what do those numbers actually mean, and how precise are the differences we talk about, like “half a stop” or “two-thirds of a stop”?
In this article, we’ll unpack how f-numbers relate to light transmission, explore why the system isn’t always as exact as it seems, and show you how to calculate these differences for yourself—or simply reference our handy table at the end.

Background

When we include alternative lens options in a review, we often highlight how much faster or slower they are compared to the lens being tested. For example, we might note that Lens A is half a stop faster, or that Lens B is one and a half stops slower.

However, these figures are often only approximations. This is because lens and camera manufacturers have adopted different conventions over time, and the way aperture values are displayed doesn’t always reflect the true mathematical differences in light transmission.

Most modern digital cameras show f-stops in one-third stop increments. Some older or mechanically simpler lenses use half-stop clicks on the aperture ring and some other only full stops. Both systems are convenient but not always precise.

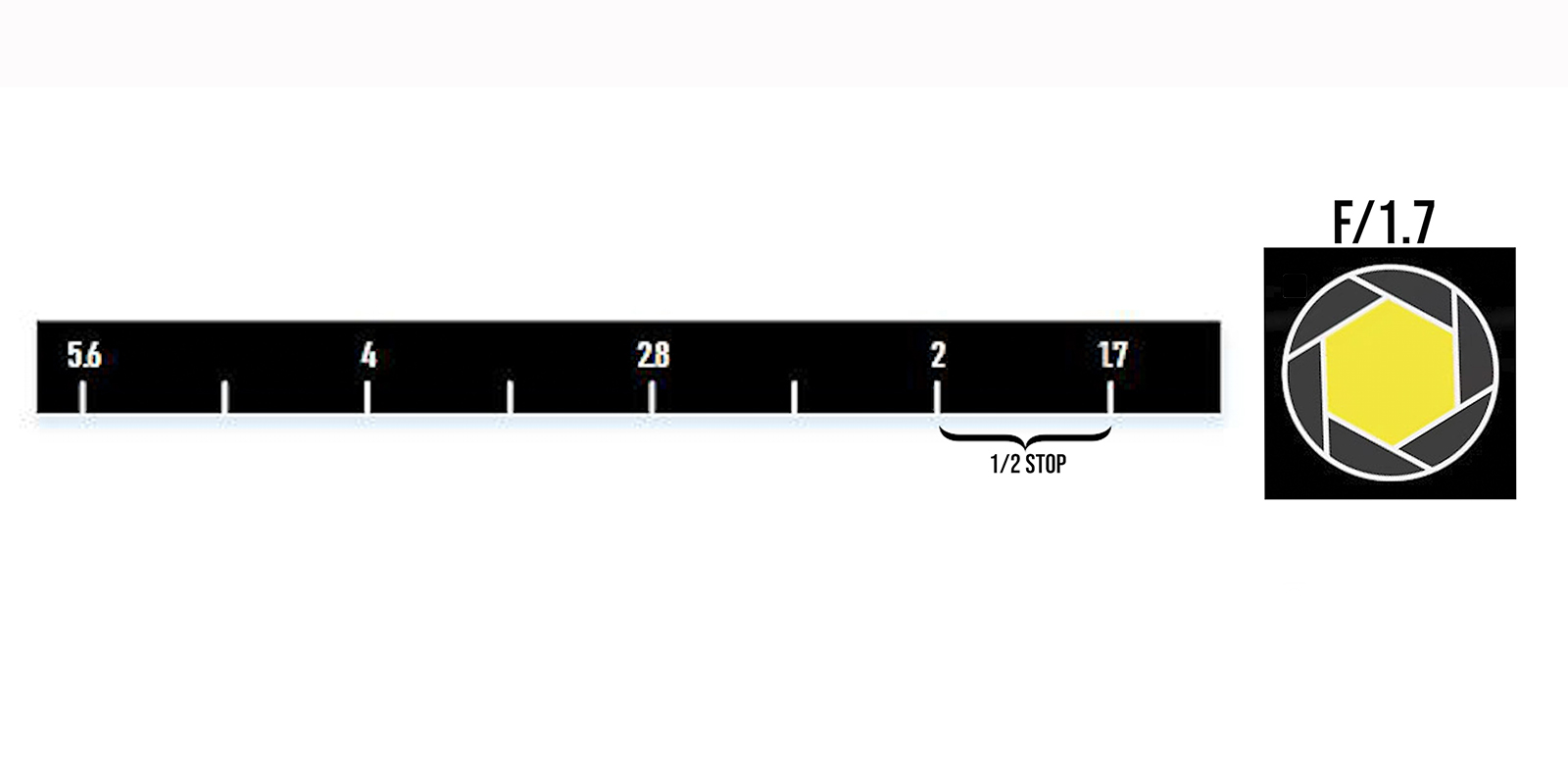
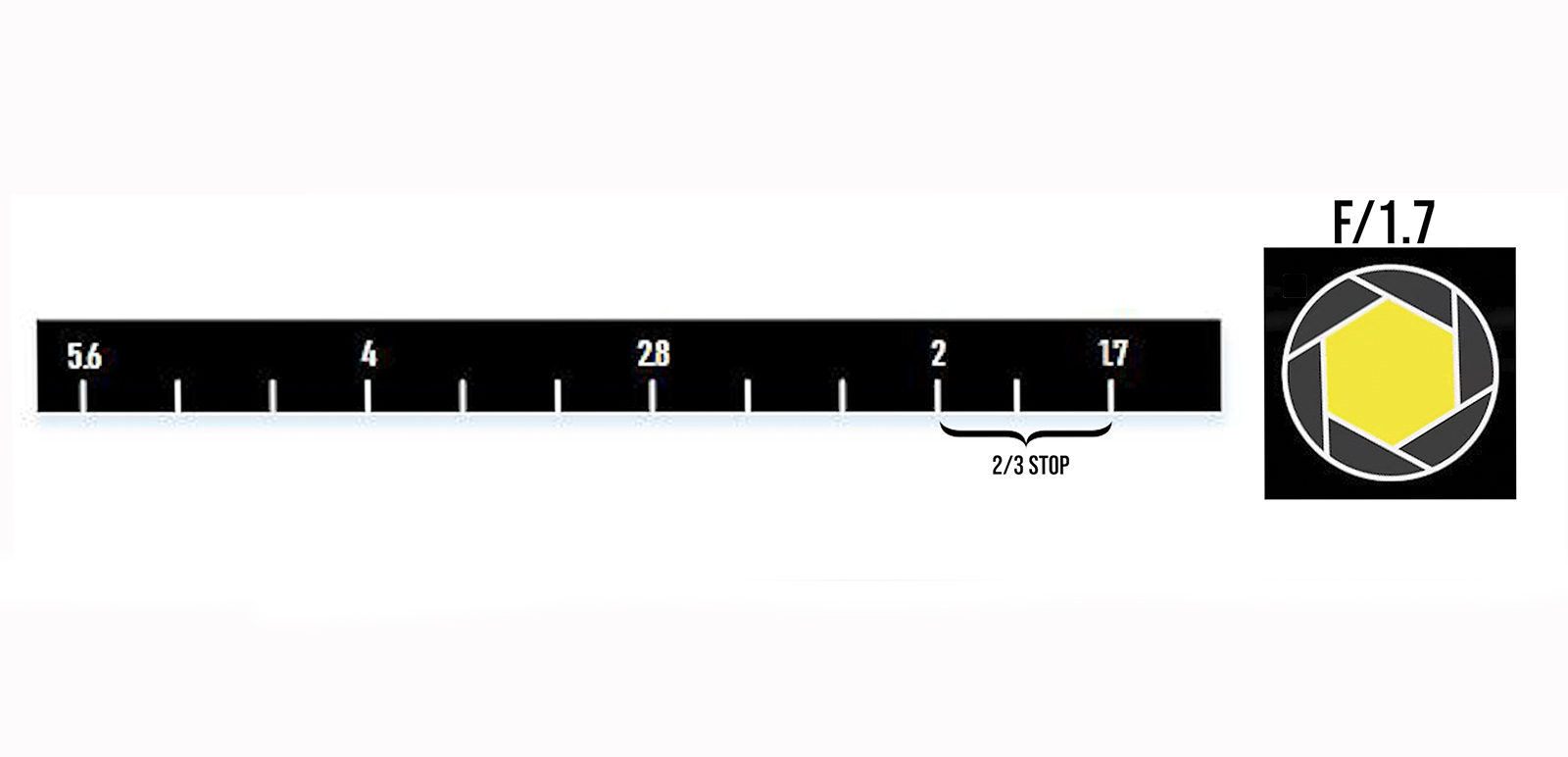
Let’s look at an example. Say you have a lens with half-stop increments and a maximum aperture of f/1.7. The next step on the ring might be f/2, implying that f/1.7 to f/2 is treated as half a stop. But what if the same lens used one-third stop steps instead—would f/1.8 appear between f/1.7 and f/2? And would that mean each step is now a third of a stop, which makes the same f/1.7 to f/2  to be treated as 2/3 stop?

These kinds of inconsistencies show how f-stop labels often reflect practical rounding rather than exact light differences.

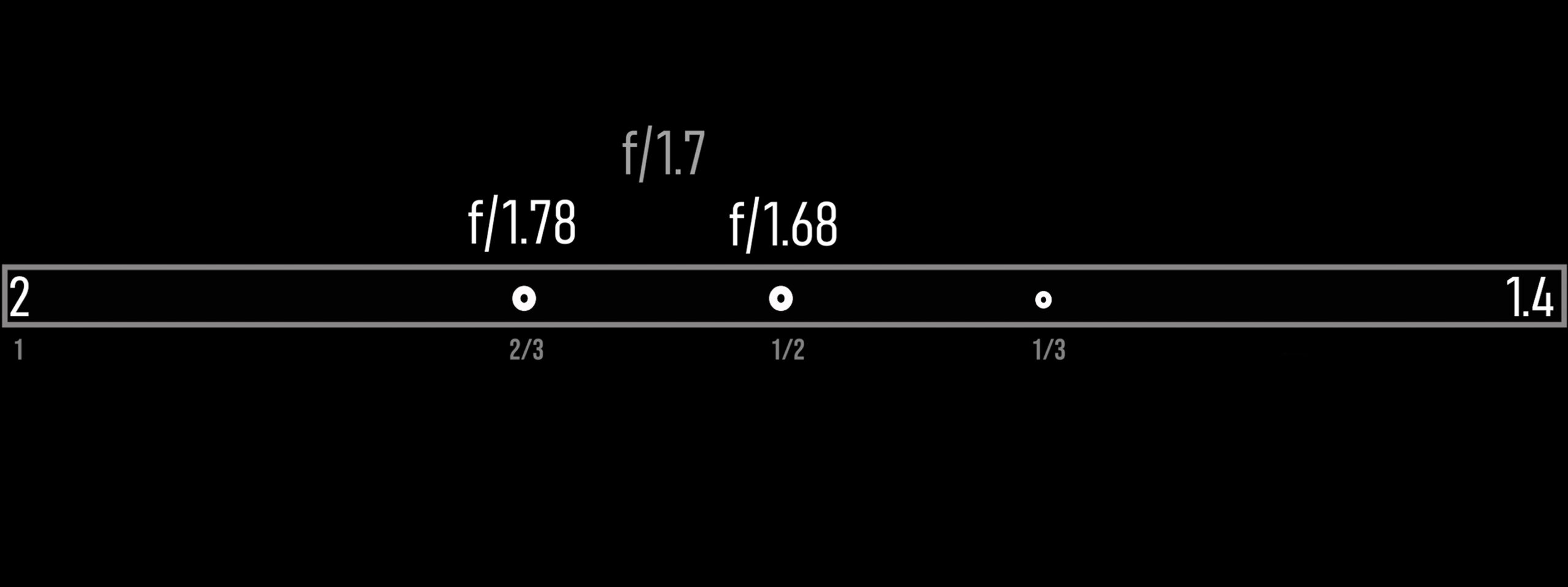
In a recent article, I wrote that a lens with an f/1.4 aperture is almost two-thirds of a stop faster than a lens with an f/1.7 aperture. I received a comment saying that this was incorrect and that the difference is actually half a stop. But the truth is, neither is exactly right.

To be precise:

• Half a stop slower than f/1.4 is f/1.68

• Two-thirds of a stop slower is f/1.78

So, f/1.7 lies between those two values. It isn’t exactly either of them.

F/1.68 is indeed closer to f/1.7 than f/1.78 is. However, since modern cameras typically show f-stops in one-third stop increments, I chose to describe the difference as almost two-thirds of a stop—to emphasise that it’s an approximation, not a precise value.

Even if we wanted to discuss such small differences, there is another factor: rounding. Most manufacturers round the focal length and f/stop values of their lenses, and sometimes graciously so.

Many f/2.0 lenses are actually closer to f/2.05, and your fancy f/1.0 lens might be f/1.05 in reality — just as most “50 mm” rangefinder lenses are around 51.6 mm.

And there is more: the f/stop usually changes with the focus distance. An f/2.8 macro lens might have the light-gathering capabilities of an f/2.8 lens at infinity, but at its minimum focus distance, it might very well be only an f/5.6 lens. On Nikon’s cameras, this will be correctly registered, but this is not the case for most other manufacturers.

On a German photography online board there is even a sticky post in the Nikon section explaining this, as people constantly complain that their pricey macro lens is slower than advertised because they do not understand the science behind it.

The Science

If you’re interested in the technical side—or want to calculate it yourself—here’s the explanation. Otherwise, feel free to skip ahead to the table below.

The f-number (f# or f-stop) of a lens is a ratio between the lens’s focal length and the diameter (D) of its aperture:

f-number = focal length / aperture diameter

( f# = focal length / D )

From that, we can also say:

D = focal length / f#

In photography, a “faster” lens means it has a larger maximum aperture—that is, a smaller f-number (f#). A larger aperture allows more light in because the opening is physically wider. Since the aperture is circular, we calculate its area (A) using the formula for the area of a circle based on its radius (r):

A = π× r²

The radius (r) is half the diameter (D), so:

A = π(D / 2)²

Or

A = (π × D²) / 4

Now, using the formula for diameter-focal length-aperture (above), we substitute:

A = (π × (focal length / f#)²) / 4

Which simplifies to:

A = (π × focal length²) / (4 × f#²)

This shows that the light entering the lens is inversely proportional to the square of the f-number, so:

• Doubling the f-number (for example, from f/4 to f/8, which is two full stops) reduces the aperture area by a factor of four, and allows one-quarter as much light in.

• Halving the f-number (for example, from f/8 to f/4, also two full stops) increases the aperture area by a factor of four, and allows four times as much light in.

This is why each full stop on the f-number scale represents either a doubling or halving of the light. The standard full-stop sequence—f/1.0, f/1.4, f/2.0, f/2.8, f/4, f/5.6, f/8, f/11, f/16, and so on—is based on multiples of the square root of 2 (√2 = 1.414). To avoid confusion, note that this is a geometric sequence and not an arithmetic one.

Because (√ 2)² = 2, each full stop means a change in light by a factor of 2, either more or less, depending on the direction.

1 × (√ 2) ≅ 1.4
1.4 × (√ 2) ≅ 2
2 × (√ 2) ≅ 2.8
..
16 × (√ 2) ≅ 22
22 × (√ 2) ≅ 32

So, now you can calculate the exact difference between f-numbers and how much faster or slower one aperture is compared to another—or you can simply refer to the table below.

Table of F-Stops and Their Exact Values

Here’s a table showing different f-stops, along with the exact values that are 1/2, 1/3, or 1/4 stops faster or slower than each one.

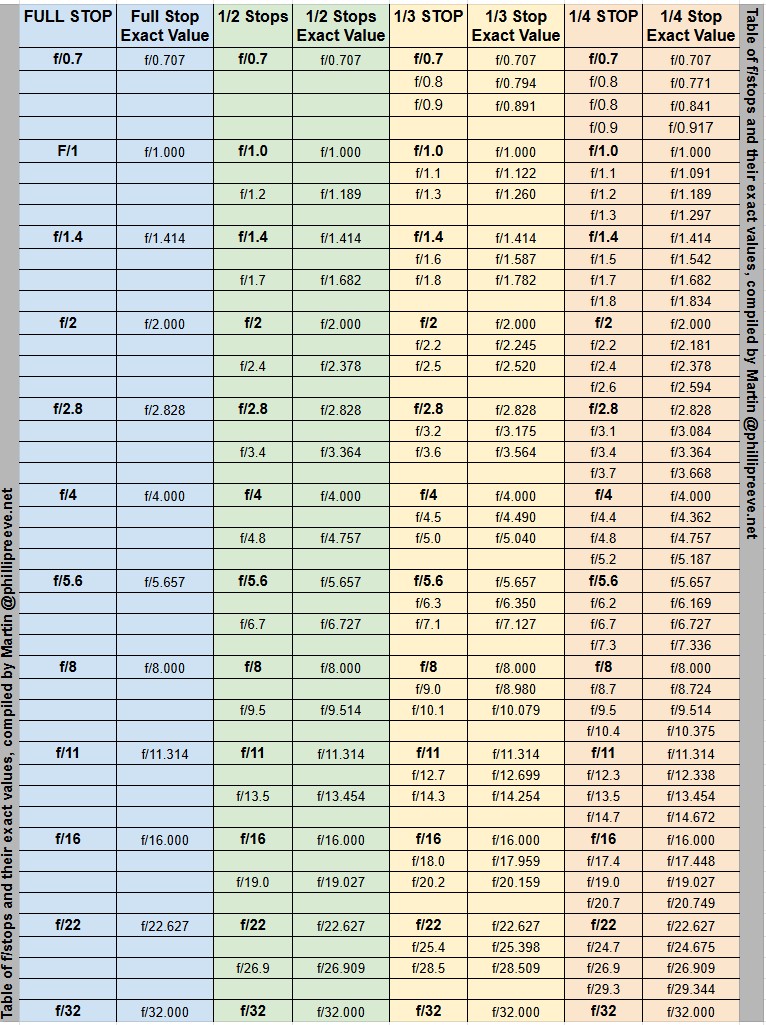
Some readers may wonder about the speed of a lens with a max aperture of f/0.95 (e.g. Nikon Z 58mm f/0.95 S Noct or Leica Noctilux-M f/0.95 ASPH), how much faster than f/1.2 are they?

Well, f/0.95 is only about 1/7 stop faster than f/1.0 and approximately 0.67 stops faster than a f/1.2 lens, i.e., about 2/3 stop.

Fun facts

The Fastest Lens Ever Made

The fastest lens ever made is the Carl Zeiss Planar 50mm f/0.7. Developed in 1966 for a very specific purpose, this lens was acquired by NASA for its Apollo lunar missions. A persistent rumor suggests the lens was designed to photograph the far side of the Moon in extremely low light, but this has never been confirmed and is widely considered a myth. Only ten units of the f/0.7 lens were ever produced, and it was never made commercially available; it was strictly a special-order item.

One of the most famous stories surrounding the Zeiss Planar 50mm f/0.7 lens is its use by film director Stanley Kubrick for his 1975 film Barry Lyndon. Kubrick reportedly acquired three of these lenses to shoot scenes lit primarily by candlelight – a groundbreaking cinematic technique at the time due to the lens’s exceptionally wide f/0.7 aperture, which allowed him to capture images in very low light. This work won the film four Academy Awards, including Best Cinematography. Today it might not sound that impressive, but back then it was done on film cameras with complex moving shots—not just simple still images—which was a remarkable feat for the time.

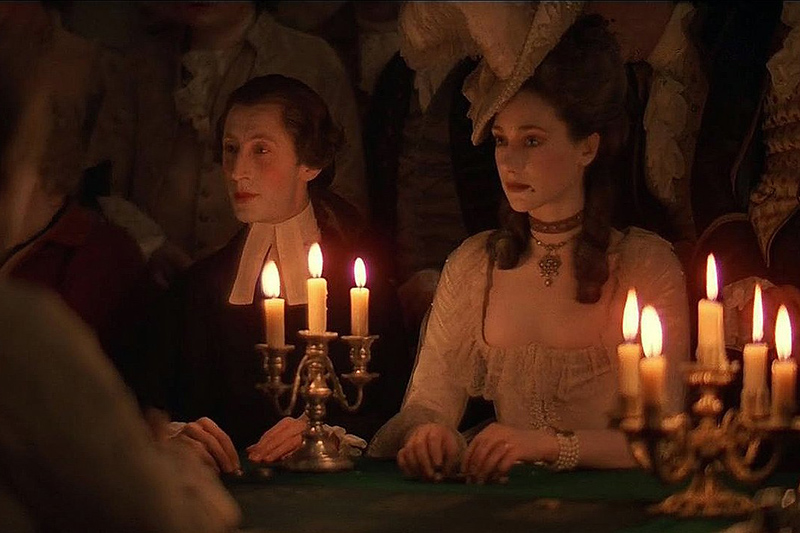
However, the rumor that Kubrick acquired the lenses from NASA is also a myth; Zeiss sold the lenses directly to Kubrick’s production company. According to Zeiss, ten lenses were produced: six were sold to NASA, three to Stanley Kubrick, and one was retained by Zeiss.

The Fastest Commercially Available Lens

You may ask about the fastest commercially available lens:  The Voigtländer 29mm  f/0.8 Super Nokton aspherical, exclusively for the Micro-Four-Thirds standard, and is the world’s first production lens with a speed of F0.8 at its introduction, November 2020.

For a larger format you can get the second fastest lens, available for APS-C cameras, the Kipon Ibelux 40mm f/0.85 Mk III. Now in its third iteration, it’s priced around $1,800 and is available for Fuji X, Nikon Z, Canon RF, Sony E, L-Mount, Canon EF-M, and Micro Four Thirds mounts.

Further Reading

What camera gear and accessories do I use most frequently?

Support Us

Did you learn something new, find this article useful, or simply enjoy reading it? We’ve put a lot of time and resources into creating it, and your support helps us keep going. If you’d like to show your appreciation, please consider clicking the Donate button!

(Donations via Paypal or bank card)

What’s in my camera bag?  MY 2024 KIT!!

• Main camera : https://amzn.to/3TsGtKg
• Camera grip : https://amzn.to/4e0G3CR
• Memory Card 1: https://amzn.to/47pA20i
• Memory Card 2 : https://amzn.to/3XHYxlZ 
• Camera 2 : https://amzn.to/3Xifou8
• Camera grip: https://amzn.to/4dYYpV9
• Memory card 1: https://amzn.to/4e5h2H0
• Memory card 2: https://amzn.to/3zu7W7n
• Small travel tripod: https://amzn.to/4goIX68
  
• Mini tripod: https://amzn.to/4e09XXX
• Small shoulder bag: https://amzn.to/47tPMiY
• Medium shoulder bag: https://amzn.to/4ej4bjY

This site contains affiliate links, for which I may receive a small commission if you purchase via the links at no additional cost to you. This helps support the creation of future content.

The following two tabs change content below.

• Bio
• Latest Posts

Martin

Martin M.H. lives outside Stockholm, Sweden. He is a M.Sc. in Computer Technology but he has been a passionate photographer for over 50 years. He started his photographic adventures when he was thirteen with an Agfamatic pocket camera, which he soon replaced with a Canon rangefinder camera that his mom gave him in his teenages. After that he has been using Canon SLR, Nikon SLR manual focus and Autofocus, Sony mirrorless crop sensor, Nikon DSLR and Nikon Mirrorless. He has photographed any genre he could throughout the years and you can see all kind of images in his portfolio. During the later years though it has been mostly landscape, nature, travel and some street/documentary photography.

Latest posts by Martin (see all)

• REVIEW: 7Artisans AF 35mm f/1.8 - October 15, 2025
• REVIEW: Nikon AI Nikkor 24mm f/2 - October 12, 2025
• REVIEW: Viltrox Spark Z3 Flash - October 10, 2025